Java8函数式编程篇五之数据并行化

/ Java函数式编程Lambda / 没有评论 / 2571浏览

Java8Lambda并行

第 6 章 数据并行化

本章主要内容并不在于如何更改代码，而是讲述为什么需要并 行化和什么时候会带来性能的提升。要提醒大家的是，本章并不是关于 Java 性能的泛泛之谈，我们只关注 Java 8 轻松提升性能的技术。

6.1 并行和并发

并发是两个任务共享时间段，并行则是两个任务在同一时间发生，比如运行在多核 CPU 上。如果一个程序要运行两个任务，并且只有一个 CPU 给它们分配了不同的时间片，那么这就是并发，而不是并行。两者之间的区别如下图所示。

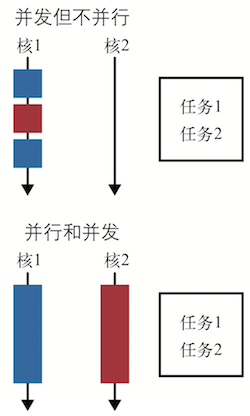
并发和并行的区别

并行化是指为缩短任务执行时间，将一个任务分解成几部分，然后并行执行。这和顺序执行的任务量是一样的，区别就像用更多的马来拉车，花费的时间自然减少了。实际上，和顺序执行相比，并行化执行任务时，CPU 承载的工作量更大。

本章会讨论一种特殊形式的并行化:数据并行化。数据并行化是指将数据分成块，为每块数据分配单独的处理单元。还是拿马拉车那个例子打比方，就像从车里取出一些货物，放到另一辆车上，两辆马车都沿着同样的路径到达目的地。

当需要在大量数据上执行同样的操作时，数据并行化很管用。它将问题分解为可在多块数据上求解的形式，然后对每块数据执行运算，最后将各数据块上得到的结果汇总，从而获得最终答案。

人们经常拿任务并行化和数据并行化做比较，在任务并行化中，线程不同，工作各异。我 们最常遇到的Java EE应用容器便是任务并行化的例子之一，每个线程不光可以为不同用 户服务，还可以为同一个用户执行不同的任务，比如登录或往购物车添加商品。

6.2 为什么并行化如此重要

在过去十年中，主流的芯片厂商转向了多核处理器。服务器通过几个物理单元搭载 32 或 64 核的情况已不鲜见，而且，这种趋势尚无减弱的征兆。这种变化影响到了软件设计。我们不能再依赖提升 CPU 的时钟频率来提高现有代码的计算能力，需要利用现代 CPU 的架构，而这唯一的办法就是编写并行化的代码。

阿姆达尔定律是一个简单规则，预测了搭载多核处理器的机器提升程序速度的理论最大值。以一段完全串行化的程序为例，如果将其一半改为并行化处理，则不管增加多少处理器，其理论上的最大速度只是原来的 2 倍。有了大量的处理器后，现在这已经是现实了，问题的求解时间将完全取决于它可被分解成几个部分。

以这样的方式思考性能问题，优化任何和计算相关的任务立即变成了如何有效利用现有硬件的问题。当然，不是所有的任务都和计算相关，本章只关注这类和计算相关的问题。

6.3 并行化流操作

并行化操作流只需改变一个方法调用。如果已经有一个 Stream 对象，调用它的 parallel 方法就能让其拥有并行操作的能力。如果想从一个集合类创建一个流，调用 parallelStream 就能立即获得一个拥有并行能力的流。

让我们先来看一个具体的例子,计算了一组专辑的曲目总长度。它拿到每张专辑的 曲目信息，然后得到曲目长度，最后相加得出曲目总长度。

public int serialArraySum() { return albums.stream()
                      .flatMap(Album::getTracks)
                      .mapToInt(Track::getLength)
                      .sum();
}

    public int parallrlArraySum(List<Album> albums) {
        return albums.parallelStream()
                .flatMap(Album::getTracks)
                .mapToInt(Track::getLength)
                .sum();
    }

读到这里，大家的第一反应可能是立即将手头代码中的 stream 方法替换为 parallelStream 方法，因为这样做简直太简单了!先别忙，为了将硬件物尽其用，利用好并行化非常重要，但流类库提供的数据并行化只是其中的一种形式。

我们先要问自己一个问题:并行化运行基于流的代码是否比串行化运行更快?这不是一个简单的问题。回到前面的例子，哪种方式花的时间更多取决于串行或并行化运行时的环境。

中的代码为准，在一个四核电脑上，如果有 10 张专辑，串行化代码的速 度是并行化代码速度的 8 倍;如果将专辑数量增至 100 张，串行化和并行化速度相当;如 果将专辑数量增值 10000 张，则并行化代码的速度是串行化代码速度的 2.5 倍。

输入流的大小并不是决定并行化是否会带来速度提升的唯一因素，性能还会受到编写代码的方式和核的数量的影响。6.6 节会详述和性能有关的细节，但现在还是再来看一个更复杂的例子吧。

6.4 模拟系统

并行化流操作的用武之地是使用简单操作处理大量数据，比如模拟系统。本节我们会搭建一个简易的模拟系统来理解摇骰子，但其中的原理对于大型、真实的系统也适用。

我们这里要讨论的是蒙特卡洛模拟法。蒙特卡洛模拟法会重复相同的模拟很多次，每次模拟都使用随机生成的种子。每次模拟的结果都被记录下来，汇总得到一个对系统的全面模拟。蒙特卡洛模拟法被大量用在工程、金融和科学计算领域。

如果公平地掷两次骰子，然后将赢的一面上的点数相加，就会得到一个 2~12 的数字。点数的和至少是 2，因为骰子六个面上最小的点数是 1，而我们将骰子掷了两次;点数的和最大超不过 12，因为骰子点数最多的一面也不过 6 点。我们想要得出点数落在 2~12 之间 每个值的概率。

解决该问题的方法之一是求出掷骰子的所有组合，比如，得到 2 点的方式是第一次掷得 1 点，第二次也掷得 1 点。总共有 36 种可能的组合，因此，掷得 2 点的概率就是 1/36。

另外一种解法是使用 1 到 6 的随机数模拟掷骰子事件，然后用得到每个点数的次数除以总的投掷次数。这就是一个简单的蒙特卡洛模拟。模拟投掷骰子的次数越多，得到的结果越准确，因此，我们希望尽可能多地增加模拟次数。

如下代码展示了如何使用流实现蒙特卡洛模拟法。N 代表模拟次数，在➊处使用 IntStream 的range方法创建大小为N的流，在➋处调用parallel方法使用流的并行化操作， twoDiceThrows 函数模拟了连续掷两次骰子事件，返回值是两次点数之和。在➌处使用 mapToObj 方法以便在流上使用该函数。

    public static final Integer N = 4;

    public static Map<Integer, Double> parallelDiceRolls() {
        IntFunction<Integer> intFunction = (a) -> (int) (1 + Math.random() * (6 - 1 + 1)) + (int) (1 + Math.random() * (6 - 1 + 1));
        double fraction = 1.0 / N;
        return IntStream.range(0, N)                   ①
                .parallel()                            ②
                .mapToObj(intFunction)                 ③
                .collect(groupingBy(side -> side,      ④
                        summingDouble(n -> fraction)));⑤
    }

在➍处得到了需要合并的所有结果的流，使用前一章介绍的 groupingBy 方法将点数一样 的结果合并。我说过要计算每个点数的出现次数，然后除以总的模拟次数 N。在流框架中， 将数字映射为 1/N 并且相加很简单，这和前面说的计算方法是等价的。在➎处我们使用 summingDouble方法完成了这一步。最终的返回值类型是Map<Integer, Double>，是点数之 和到它们的概率的映射。

个人理解： ①产生 0 - （N-1）的流 ②调用parallel方法使用流的并行化操作 ③Lambda 模拟两次掷骰子和，并返回结果 ④⑤根据元素的值groupby，summingDouble(n -> fraction) 出现多少次，就加多少个 1.0 / N，也就是出现的概率。summingDouble就是简单计算和。

我得承认这段代码不算儿戏，但使用 5 行代码即能实现蒙特卡洛模拟法还是很精巧的。重要的是模拟的次数越多，得到的结果越准确，因此我们运行多次模拟的动机就会更加强烈。这是一个很好的并行化案列，并行化能带来速度的提升。

我已经带领读者浏览了整个实现细节，为了对比，下面的代码给出了手动实现并行化蒙特卡洛模拟法的代码。可以看到，大多数代码都在处理调度和等待线程池中的某项任务完成。而 使用并行化的流时，这些都不用程序员手动管理。

//代码太多了，这里就不全部列出来了，具体可参看原文
public class ManualDiceRolls {
private static  nal int N = 100000000;
private  nal double fraction;
private  nal Map<Integer, Double> results; private  nal int numberOfThreads;
private  nal ExecutorService executor; private  nal int workPerThread;
public static void main(String[] args) { 
ManualDiceRolls roles = new ManualDiceRolls(); 
roles.simulateDiceRoles();
    }
public ManualDiceRolls() {
fraction = 1.0 / N;
results = new ConcurrentHashMap<>();
numberOfThreads = Runtime.getRuntime().availableProcessors(); 
executor = Executors.newFixedThreadPool(numberOfThreads); 
workPerThread = N / numberOfThreads;
    }
 ......

6.5 限制

之前提到过使用并行流能工作，但这样说有点无耻。虽然只需一点改动，就能让已有代码并行化运行，但前提是代码写得符合约定。为了发挥并行流框架的优势，写代码时必须遵守一些规则和限制。

之前调用 reduce 方法，初始值可以为任意值，为了让其在并行化时能工作正常，初值必须 为组合函数的恒等值。拿恒等值和其他值做 reduce 操作时，其他值保持不变。比如，使用 reduce 操作求和，组合函数为(acc, element) -> acc + element，则其初值必须为 0，因为任何数字加 0，值不变。

reduce 操作的另一个限制是组合操作必须符合结合律。这意味着只要序列的值不变，组合操作的顺序不重要。有点疑惑?别担心!请看如下代码，我们可以改变加法和乘法的顺序， 但结果是一样的。

(4+2)+1=4+(2+1)=7
(4*2)*1=4*(2*1)=8

要避免的是持有锁。流框架会在需要时，自己处理同步操作，因此程序员没有必要为自己的数据结构加锁。如果你执意为流中要使用的数据结构加锁，比如操作的原始集合，那么有可能是自找麻烦。

在前面我还解释过，使用 parallel 方法能轻易将流转换为并行流。如果读者在阅读本书的同时，还查看了相应的 API，那么可能会发现还有一个叫 sequential 的方法。在要对流求值时，不能同时处于两种模式，要么是并行的，要么是串行的。如果同时调用了 parallel 和 sequential 方法，最后调用的那个方法起效。

6.6 性能

在前面我简要提及了影响并行流是否比串行流快的一些因素，现在让我们仔细看看它们。 理解哪些能工作、哪些不能工作，能帮助在如何使用、什么时候使用并行流这一问题上做出明智的决策。影响并行流性能的主要因素有 5 个，依次分析如下。

使用并行流框架，理解如何分解和合并问题是很有帮助的。这让我们能够知悉底层如何工作，但却不必了解框架的细节。

来看一个具体的问题，看看如何分解和合并它。下面并行求和的代码。

private int addIntegers(List<Integer> values) { 
    return values.parallelStream()
                      .mapToInt(i -> i)
                      .sum();
}

在底层，并行流还是沿用了 fork/join 框架。fork 递归式地分解问题，然后每段并行执行， 最终由 join 合并结果，返回最后的值。过程如下图所示：

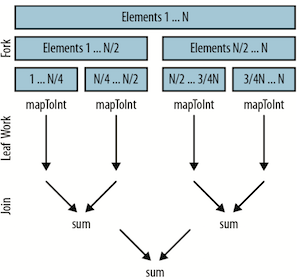
流并行处理

假设并行流将我们的工作分解开，在一个四核的机器上并行执行。

  1. 数据被分成四块。
  2. 计算工作在每个线程里并行执行。这包括将每个 Integer 对象映射为 int 值，然后在每个线程里将 1/4 的数字相加。理想情况下，我们希望在这里花的时间越多越好，因为这里是并行操作的最佳场所。
  3. 然后合并结果。在上面的并行求和代码中，就是 sum 操作，但这也可能是 reduce、collect 或其他终结操作。

根据问题的分解方式，初始的数据源的特性变得尤其重要，它影响了分解的性能。直观上 看，能重复将数据结构对半分解的难易程度，决定了分解操作的快慢。能对半分解同时意味着待分解的值能够被等量地分解。

我们可以根据性能的好坏，将核心类库提供的通用数据结构分成以下 3 组。

初始的数据结构影响巨大。举一个极端的例子，对比对 10000 个整数并行求和，使用 ArrayList 要比使用 LinkedList 快 10 倍。这不是说业务逻辑的性能情况也会如此，只是说明了数据结构对于性能的影响之大。使用形如 LinkedList 这样难于分解的数据结构并行运行可能更慢。

理想情况下，一旦流框架将问题分解成小块，就可以在每个线程里单独处理每一小块，线程之间不再需要进一步通信。无奈现实不总遂人愿!

在讨论流中单独操作每一块的种类时，可以分成两种不同的操作:无状态的和有状态的。 无状态操作整个过程中不必维护状态，有状态操作则有维护状态所需的开销和限制。

如果能避开有状态，选用无状态操作，就能获得更好的并行性能。无状态操作包括 map、 filter 和 flatMap，有状态操作包括 sorted、distinct 和 limit。

6.7 并行化数组操作

Java 8 还引入了一些针对数组的并行操作，脱离流框架也可以使用 Lambda 表达式。像流框架上的操作一样，这些操作也都是针对数据的并行化操作。让我们看看如何使用这些操作解决那些使用流框架难以解决的问题。

这些操作都在工具类 Arrays 中，该类还包括 Java 以前版本中提供的和数组相关的有用方法，下表总结了新增的并行化操作。

方法名操作
parallelPrefix任意给定一个函数，计算数组的和
parallelSetAll使用 Lambda 表达式更新数组元素
parallelSort并行化对数组元素排序

使用一个 for 循环初始化数组。在这里，我们用数 组下标初始化数组中的每个元素。

public static double[] imperativeInitilize(int size) { 
    double[] values = new double[size];
    for(int i = 0; i < values.length;i++) {
        values[i] = i;
    }
return values; 
}

使用 parallelSetAll 方法能轻松地并行化该过程，代码如下所示。首先提供了一个用于操作的数组，然后传入一个 Lambda 表达式，根据数组下标计算元素的值。在该例中， 数组下标和元素的值是一样的。使用这些方法有一点要小心:它们改变了传入的数组，而没有创建一个新的数组。

    public static double [] parallelInitialize(int size){
        double [] values = new double[size];
        Arrays.parallelSetAll(values,i ->i);
        return values;
    }

parallelPrefix 操作擅长对时间序列数据做累加，它会更新一个数组，将每一个元素替换为当前元素和其前驱元素的和，这里的“和”是一个宽泛的概念，它不必是加法，可以是任意一个 BinaryOperator。

使用该方法能计算的例子之一是一个简单的滑动平均数。在时间序列上增加一个滑动窗口，计算出窗口中的平均值。如果输入数据为 0、1、2、3、4、3.5，滑动窗口的大小为 3，则简单滑动平均数为 1、2、3、3.5。如下代码展示了如何计算滑动平均数。

    public static double[] simpleMovingAverage(double[] values, int n) {
        //不影响原数组，先拷贝一份
        double[] sums = Arrays.copyOf(values, values.length); ①
        //每一个元素替换为当前元素和其前驱元素的和
        Arrays.parallelPrefix(sums, Double::sum);②
        int start = n - 1;
        //range的作用其实就是产生遍历的下标
        return IntStream.range(start, sums.length)③
                .mapToDouble(i -> {
                    //第一个窗口的前一个值不存在因此为0
                    double prefix = i == start ? 0 : sums[i - n];
                    return (sums[i] - prefix) / n;④
                }).toArray();⑤
    }

这里要理解滑动平均值的求法，是先计算和（每一个元素替换为当前元素和其前驱元素的和）然后减去窗口起始位置的元素即可，除以 n 即得到平均值。

这段代码有点复杂，我会分步介绍它是如何工作的。参数 n 是时间窗口的大小，我们据此 计算滑动平均值。由于要使用的并行操作会改变数组内容，为了不修改原有数据，在➊处 复制了一份输入数据。

在➋处执行并行操作，将数组的元素相加。现在 sums 变量中保存了求和结果。比如输入 0、1、2、3、4、3.5，则计算后的值为 0.0、1.0、3.0、6.0、10.0、13.5。

现在有了和，就能计算出时间窗口中的和了，减去窗口起始位置的元素即可，除以 n 即得到 平均值。可以使用已有的流中的方法计算该值，那就让我们来试试吧!使用 Intstream.range 得到包含所需元素下标的流。

在➍处使用总和减去窗口起始值，然后再除以 n 得到平均值。最后在➎处将流转换为数组。

6.8 要点回顾

6.9 练习

  1. 下面的代码顺序求流中元素的平方和，将其改为并行处理。
public static int sequentialSumOfSquares(IntStream range) {
     return range.map(x -> x * x).sum();
}

    public static int parallelSumOfSquares(IntStream range) {
        return range.parallel()
                .map(x -> x * x).sum();
    }
  1. 下面代码把列表中的数字相乘，然后再将所得结果乘以 5。顺序执行这段程序没有问题，但并行执行时有一个缺陷，使用流并行化执行该段代码，并修复缺陷。
public static int multiplyThrough(List<Integer> linkedListOfNumbers) { 
    return linkedListOfNumbers.stream()
                       .reduce(5, (acc, x) -> x * acc);
}

    public static int multiplyThrough(List<Integer> linkedListOfNumbers) {
        return linkedListOfNumbers.parallelStream()
                .reduce(1, (acc, x) -> x * acc) * 5;
    }
  1. 如下代码计算列表中数字的平方和。尝试改进代码性能，但不得牺牲代码质量。 只需要一些简单的改动即可。
public int slowSumOfSquares() {
    return linkedListOfNumbers.parallelStream()
                                .map(x->x*x)
                                .reduce(0, (acc, x) -> acc + x);
}

public int slowSumOfSquares() {
    return linkedListOfNumbers.parallelStream()
                                .map(x->x*x)
                                .sum();
}

本文由 zealzhangz 创作，采用 知识共享署名4.0 国际许可协议进行许可
本站文章除注明转载/出处外，均为本站原创或翻译，转载前请务必署名
最后编辑时间为: 2018/11/08 21:00

→ ← ↓ ↑